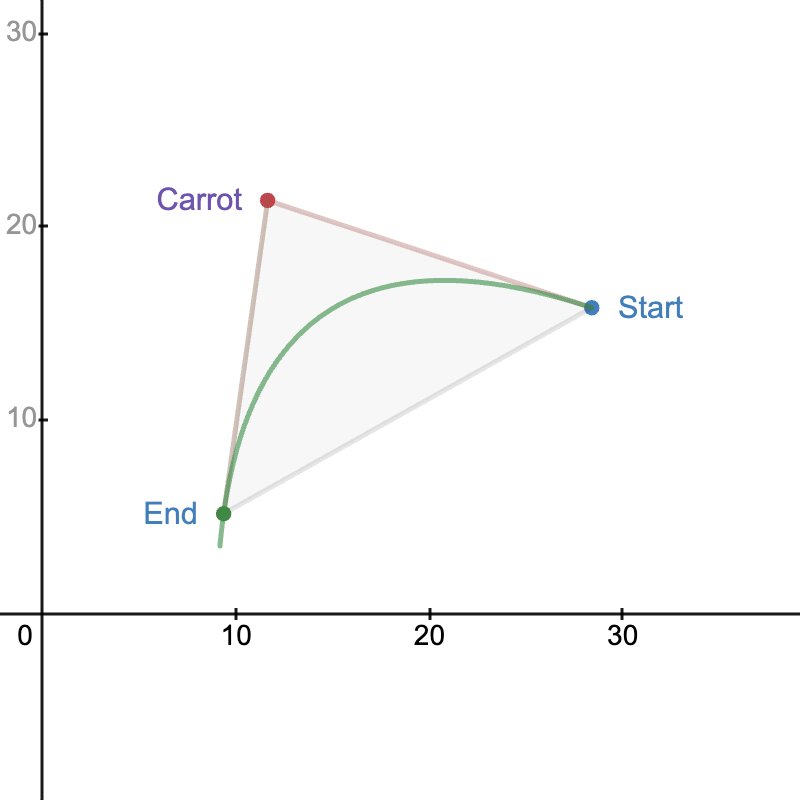
Boomerang Controller
To begin with, the Boomerang Controller is not a control algorithm on its own. To call it that assumes that the Boomerang Controller can get to the targets on its own.
Boomerang Controller is an odometry-based algorithm that that with the target,theta, and dleadcan tell the robot how to get to the target coordinate at the target angle in a controlled manner.
This means that instead of the Boomerang Controller outputting the motor power at the loopback time, a coordinate called the carrot point is outputted. Using the other real control algorithms, the robot should be traveling to the carrot point at all times to construct the curve.
Coordinate Class
It is reccomended to create a c++ class for coordinates to make caculations simpler. It can be done like so:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <cmath> // math functions like sqrt()
// provides information about the properties of arithmetic types
#include <limits>
class Point {
public:
// values at any point
float x;
float y;
/* theta is initialized at NaN so theta does not
need to be inputted */
float theta = std::numeric_limits<float>::quiet_NaN();
// Constructor
Point(float x, float y, float theta = std::numeric_limits<float>::quiet_NaN())
: x(x),
y(y),
theta(theta) {}
// Method to calculate distance between two points
float distanceTo(const Point& other) const {
float deltaX = x - other.x;
float deltaY = y - other.y;
return sqrt(deltaX * deltaX + deltaY * deltaY);
}
// Method to convert degrees to radians float
degreesToRadians(float degrees) { return degrees * M_PI / 180.0;}
// angular error
float angleError(const Point& other) { return other.theta - theta; }
};
Example
1
2
3
4
5
6
7
8
9
int main() {
Point p1(3.0, 4.0);
Point p2(6.0, 8.0);
std::cout << "Distance between p1 and p2: " << p1.distanceTo(p2) << std::endl;
Point p3(10, 4, 90);
Point p4(6, 12, 180);
std::cout << "Angle between p3 and p4: " << p3.angleError(p4) << std::endl;
}
Finding The Carrot Point
In order to find the carrot point, the coordinates of a point rotating around another point with a variables distance must be found.
Rotating A Point Around The Origin
To begin with, a point can be rotated around the origin with this simple equation: \(\left(\cos\left(\theta\right),\sin\left(\theta\right)\right)\)
This is because on the unit circle, \(\cos\theta=x\) \(\sin\theta=y\) The distance from the point and the origin is
1because the unit circle radius is1
To change the distance of the coordinate from the origin, the coordinate can simply be multiplied by the radius or distance from the origin desired.
\[\left(d\cdot\cos\left(\theta\right),d\cdot\sin\left(\theta\right)\right)\]Where d is the distance.
c++ example:
1
Point newPoint(d * cos(theta),d * sin(theta));
Rotating A Point around Another Point
This can be done by subtracting the new coordinate by the reference coordinate. \(\left(Target_x-d\cos\left(\theta\right),Target_y-d\sin\left(\theta\right)\right)\)
c++ example:
1
2
3
4
5
Point target(10,10);
Point newPoint(
target.x - d * cos(theta),
target.y - d * sin(theta)
);
The d value of the distance of the carrot point should be variable scaled. The simplest way to do that is by making d equal to the distance of the start and end point. \(d=\sqrt{\left(robot_x-target_x\right)^{2}+\left(robot_y-target_y\right)^{2}}\) From the Point class:
1
2
3
4
5
float distanceTo(const Point& other) const {
float deltaX = x - other.x;
float deltaY = y - other.y;
return sqrt(deltaX * deltaX + deltaY * deltaY);
}
$d_{lead}$
There is one more calculation for the carrot point, $d_{lead}$.
$d_{lead}$ is simply a constant that normally fits under the restriction $\left{0\le d_{lead}\le1\right}$ and multiplies d.
Larger $d_{lead}$ leads to higher curvature in the path. \(\left(Target_{x}-d\cos\left(\theta\right)\cdot d_{lead},Target_{y}-d\sin\left(\theta\right)\cdot d_{lead}\right)\)
Basic Code Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <cmath> // math functions like sqrt()
// provides information about the properties of arithmetic types
#include <limits>
class Point {
public:
// values at any point
float x;
float y;
/* theta is initialized at NaN so theta does not
need to be inputted */
float theta = std::numeric_limits<float>::quiet_NaN();
// Constructor
Point(float x, float y, float theta = std::numeric_limits<float>::quiet_NaN())
: x(x),
y(y),
theta(theta) {}
// Method to calculate distance between two points
float distanceTo(const Point& other) const {
float deltaX = x - other.x;
float deltaY = y - other.y;
return sqrt(deltaX * deltaX + deltaY * deltaY);
}
// Method to convert degrees to radians float
degreesToRadians(float degrees) { return degrees * M_PI / 180.0; }
// angular error
float angleError(const Point& other) { return other.theta - theta; }
};
void boomerang(float x, float y, float theta, float dlead) {
// assuming you have a PID class
PID linearPID(4, 0, 6) PID angularPID(1, 0, 2);
float linearError;
float linearPower;
float angularError;
float angularPower;
// calculate target pose in standard form
Pose target(x, y, M_PI_2 - degreesToRadians(theta));
while (!angularSettled && !linearSetted) {
Point carrot(target.x - d * cos(theta) * dlead,
target.y - d * sin(theta) * dlead);
linearError = robot.distanceTo(carrot);
linearPower = linearPID.update(linearError);
angularError = robot.angleTo(theta);
angularPower = angularPID.update(angularError);
float leftPower = linearPower + angularPower;
float rightPower = linearPower - angularPower;
/* move the drivetrain
(assuming you have motor groups for each sandwich) */
drivetrain.leftMotors->move(leftPower);
drivetrain.rightMotors->move(rightPower);
}